METHODIK

Ganzheitliche Methodik - Ausgangslage
#1 Es gibt nur eine Lösung?
#2 Alles ist so kompliziert?
#3 Bestehende Regeln sind einzuhalten?
#4 Einschätzung anderer Spieler?
#5 Strategiebewertung?
#6 Kriterien Entscheidungsfindung?

#1 Alternativlosigkeit
In einer komplexen Welt gibt es eine unendliche Anzahl möglicher Pfade und Bewertungen. Die Verengung des Lösungsraumes ist oft die Folge von Zeit- und Ressourcenmangel bzw. ideologischer, ethischer oder intellektueller Grenzen. Kompetente Analysen schließen nichts aus und nehmen Konsequenzen gedanklich vorweg.
Fazit: Was nicht vorstellbar ist, wird auch nicht realisierbar sein!

#2 Komplexität
Komplexe Situationen sind durch eine große Zahl sich gegenseitig beeinflussender Faktoren bestimmt. Einfache, deterministische Erklärungen und Handlungsansätze greifen meist zu kurz. Entscheidungsstärke besteht in vorausschauender Investition in Lösungskompetenz, Robustheit & Resilienz bevor Probleme auftreten.
Fazit: Herausforderungen und Chancen vorherzusehen ist die Kunst!

#3 Regeln
Regeln und Grenzen sollen einer ganzheitlichen Entwicklung dienen und schränken den Lösungsraum zugunsten Einzelner oder Vieler ein. Wenn Regeln sinnvolle Entwicklungen behindern oder zu einer ungerechtfertigten Benachteiligung führen, sind sie anzupassen oder abzuschaffen. Voraussetzung dafür sind Nachweis und Akzeptanz.
Fazit: Regeln sind kein Selbstzweck, sondern ständig zu entwickeln!

#4 Spieltheorie
Spiele sind durch Regeln, Spieler, Strategie, Einsatz und Ergebnis definiert. Zudem ist zwischen Einzelspielen und einer Abfolge von Spielen zu unterscheiden. Eine Strategie ist dominant, wenn unabhängig von der Reaktion kein besseres Ergebnisse erzielbar, ein Nash – Gleichgewicht, wenn einseitige Abweichung nicht sinnvoll ist.
Fazit: Kooperation und/oder Konfrontation können sich auszahlen!

#5 Strategiebewertung
Ausgehend von den Zielsetzungen sind im Lösungsraum alle relevanten Strategien und sich daraus ergebenden Handlungspfade zu identifizieren. Weiters sind die Reaktionen der anderen Spieler, dominante Strategien, Gleichgewichte und Kooperationen auszuloten und die optimale Strategie (höchsten Auszahlung) zu wählen.
Fazit: Suche der optimalen Strategie im gesamten Lösungsraum!

#6 Entscheidungsfindung
Die Strategien der Spieler und Ergebnisse und können maßgebend durch die Gestaltung des Spiels beeinflusst werden. Bei Produkteffizienz optimiert jeder für sich (Neoliberal), bei Pareto-Effizienz (Statisch) ist keine Verschlechterung erlaubt, bei Kaldor-Hicks müssen Verschlechterungen kompensiert werden (Nachhaltig).
Fazit: Die Spielgestaltung definiert Handlungsraum und Ergebnis!

Stochastische Methodik - Ausgangslage
#1 Verlauf - bekannt, eindeutig, stetig?
#2 Verteilung - bekannt, eindeutig, stetig?
#3 Prognose - deterministisch?
#4 Verlauf - unbekannt, unsicher, stetig?
#5 Verteilung - unbekannt, unsicher, stetig?
#6 Prognose - stochastisch

#1 Zustandsverlauf – deterministisch
Deterministische Zustandsmodelle basieren auf der Annahme strikter Naturgesetze, bei denen nur ein Zustand zu einem Zeitpunkt erlaubt ist. Zur leichteren Verständlichkeit kann der stetige Zustand in (diskrete) Zustandsklassen (Noten) eingeteilt werden. Die Lebensdauer ist durch Ausfall oder Erreichung einer Grenze definiert.
Fazit: Ein eindeutiger stetiger Verlauf ist deterministisch!
#2 Zustandsverteilung – deterministisch
Bei deterministischem Zustandserlauf verhalten sich alle Assets oder Elemente gleich d.h. alle erreichen denselben Zustand zur selben Zeit und fallen zur selben Zeit aus. Sind die Assets oder Elemente nicht im selben Alter, folgen Ausfall und Reinvestition der Altersverteilung horizontal parallel verschoben.
Fazit: Deterministisch bedeutet, alle fallen im selben Alter aus!

#3 Zustandsprognose – deterministisch
Deterministische Zustandsprognosen sind nichttriviale, objektive und valide Vorhersagen genau eines Zustands zu einem zukünftigen Zeitpunkt bzw. von Lebensdauer und Ausfallszeitpunkt. Das Ergebnis der Prognose hängt wesentlich von den zur Verfügung stehenden Informationen sowie dem verwendeten Prognosemodell ab.
Fazit: Deterministische Prognosen geben Zeitpunkt und Zustand an!

#4 Zustandsverlauf – stochastisch
In Zustandsverläufen mit einer Vielzahl an Einflüssen und Unsicherheit sind unterschiedliche Zustände zur selben Zeit möglich. Solche zeitlich geordneten, zufälligen Vorgänge sind als stochastische Prozesse beschreibbar. Im Hoffmann-Prozess wird ein skalierbarer Zustandsverlauf über eine beliebige Ausfallsverteilung integriert.
Fazit: Ein Zustandsverlauf unter Unsicherheit ist beschreibbar!

#5 Zustandsverteilung – stochastisch
Im stochastischen Prozess zeigt die Zustandsverteilung den Anteil einer großen Zahl gleichartiger/-alter Assets im jeweiligen Zustand. Für den Einzelfall entspricht dieser Anteil der „a priori“ Wahrscheinlichkeit p zu einer Zeit t in diesem Zustand zu sein. Zum Zeitpunkt der Ø Lebensdauer ist die „a priori“ Chance zu überleben daher p=50%.
Fazit: Stochastisch bedeutet nicht alle fallen zur selben Zeit aus!

#6 Zustandsprognose – stochastisch
In der stochastischen Zustandsprognose wird das deterministische Prognoseergebnis zum Erwartungswert mit der Eintrittswahrscheinlichkeit p=0. Die Unsicherheit wird unter Berücksichtigung verfügbarer Daten über eine Ausfallverteilung f(t) beschrieben. Die Lebensdauer ergibt sich als Bandbreite im Konfidenzintervall.
Fazit: Stochastische Prognosen geben Bandbreite und Konfidenz an!

Optimierte Methodik - Ausgangslage
#1 Optimierung - Lineare Probleme?
#2 Optimierung - Integer Probleme?
#3 Optimierung - Nichtlineare Probleme?
#4 Deterministischer Lebenszyklus?
#5 Stochastischer Lebenszyklus?
#6 Lösungsfindung - Brute Force VS Heuristik?

#1 Lineare Programmierung (LP)
Im Gegensatz zu einer Reihung bedeutet optimiert, dass eine Zielfunktion maximiert/minimiert wird. Sind die funktionalen Randbedingungen RB und die Zielfunktion f(xi) linear und stetig, ist der Lösungsraum ein konvexes Polytop, mit Lösung in polynomialer Zeit entlang dessen Kanten mittels linearer Programmierung (Simplex).
Fazit: Auch große lineare Probleme sind gut berechenbar!

#2 Integer Programmierung (IP)
Wenn im durch Randbedingungen abgegrenzten Lösungsraum nur ganzzahlige Lösungen erlaubt sind, spricht man von einem Integer-Problem. In der Lebenszykluskostenrechnung entspricht dies z.B. einer Aufteilung der Zeitachse in Jahresschritte. Mixed-Integer Probleme bestehen bei Verwendung diskreter und stetiger Variablen.
Fazit: Bei ganzzahliger Optimierung sind die Probleme NP-schwer!

#3 Nichtlineare Programmierung (NLP)
Sind die Entscheidungsvariablen zwar stetig, die Randbedingungen oder Zielfunktion jedoch nichtlinear, kann der Lösungsraum sowohl konvex, als auch konkav sein. Zudem können lokale Optima auftreten und die Programmierung und Berechnung ist wesentlich aufwendiger bzw. in vielen Fällen nicht in endlicher Rechenzeit lösbar.
Fazit: Nichtlineare Probleme sind nicht immer lösbar!

#4 Optimierung deterministischer LCC
Im einfachsten Fall eines deterministischen Lebenszyklus mit Ersatz sinkt die Annuität mit zunehmender Lebensdauer bis zum Ausfall. Unter der Randbedingung einer Funktion ist die Annuität bei unmittelbarem Austausch zum Ausfallzeitpunkt ein Minimum. Verursacht der Ausfall Zusatzkosten, ist die Annuität entsprechend höher.
Fazit: Die vollständige Nutzung der Lebensdauer wäre optimal!

#5 Optimierung stochastischer LCC
Unter Unsicherheit lässt sich der Ausfallszeitpunkt nicht zweifelsfrei vorher bestimmen. Unter Risiko ohne Zusatzinformationen ergibt sich ein vorzeitiger Eingriff als optimal. Mit zusätzlichen Informationen und stochastischer Prognose ist eine ökonomisch optimale Annäherung an den „a priori“ unbekannten Ausfallszeitpunkt möglich.
Fazit: Mit stochastischer Prognose zur Lösung unter Unsicherheit!

#6 Brute force - Heuristik
Für kombinatorische Probleme geringen Umfangs ist eine erschöpfende Suche des Optimums im Lösungsraum möglich (Brute Force). Im kontinuierlichen Lösungsraum ist eine erschöpfende Suche ohne Diskretisierung nicht möglich. Durch analytisches Vorgehen und Eingrenzung/Vereinfachung ist oft dennoch eine gute Näherung möglich.
Fazit: Heuristik bedeutet intelligente Näherung an ein Optimum!

Wirtschaftlich - Ausgangslage
#1 Kostenschätzung ein/viele Vorhaben?
#2 Angemessene Preise und Prüfung?
#3 Starke/schwache Dimensionierung?
#4 Konfidenzintervalle Einheitskosten?
#5 Welche Menge zu welchen Kosten?
#6 Optimierung Bauloslänge und Timing?

#1 Kostenschätzung
Die Kosten einzelner Vorhaben können aufgrund einer Vielzahl an Faktoren erheblich nach unten und oben schwanken. Bei einer größeren Anzahl vergleichbarer Vorhaben gleicht sich die Wirkung aus und der mittlere Preis ist stabiler (zentraler Grenzwertsatz). Mit der richtigen Strategie sind zudem meist bessere Preise zu erzielen.
Fazit: Im Einzelfall gibt es eine große Bandbreite – in Summe nicht!

#2 Angemessenheit
Die Kosten ergeben sich generell aus den Faktorpreisen für Material, Arbeit, Ausrüstung, Transport etc. zuzüglich Wagnis und Gewinn. Der Preis für den Kunden ergibt sich aus Angebot und Nachfrage am Markt bzw. nach Informationsstand und Zahlungsbereitschaft. Im Fall von Absprachen sind die Preise systematisch erhöht.
Fazit: Über eine Bandbreite hinaus sind erhöhte Preise kein Zufall!
#3 Dimensionierung
Die Kosten stärkerer Dimensionierung steigen i.a. degressiv aufgrund des Fixkostenanteils. Die Minimierung der Anschaffungskosten resultiert oft in kurzer Lebensdauer und hohen jährliche Kosten. Die Lebenszykluskostenrechnung (Life Cycle Costs LCC) ergibt die optimale Dimensionierung mit minimalen jährlichen Kosten (Annuität) für jeden Zinssatz i.
Fazit: Wer billig kauft, kauft oft teuer - wer Zinsen zahlt noch teurer!

#4 Konfidenzintervalle
Die degressiv steigenden Gesamtkosten zeigen sich an den abflachenden Kosten je Einheit (Skalenerträge). Statistisch gibt es einen Konfidenzintervall (Zuverlässigkeit) für die zu erwartenden Kosten je Einheit im Einzelfall (heller, breiter) sowie im Durchschnitt (dunkler, schmäler) nach Menge.
Fazit: Der Konfidenzintervall zeigt die Zuverlässigkeit der Schätzung!

#5 Kostenfunktion
Die Gesamtkosten steigen mit der Menge des Gutes meist nicht linear, sondern vielfach degressiv aufgrund eines günstigeren Einkaufs, größerer Effizienz sowie Verteilung der Fixkosten. Mit Kostenfunktionen lässt sich dieser Zusammenhang zeigen. Günstigere Preise können zudem zum Kauf größerer Mengen veranlassen.
Fazit: Der Zusammenhang von Kosten und Menge ist systematisch!

#6 Optimierung
Wenn Gesamtkosten degressiv mit der Menge zunehmen, kann eine Bündelung von Maßnahmen vorteilhaft sein. Dies ist dann der Fall, wenn die Ersparnis der Bündelung größer als der Verlust an Lebensdauer ist. Auf diese Weise sind gegenüber den derzeit verwendeten Ansätzen der Erhaltung erhebliche Einsparungen möglich.
Fazit: Innovative Optimierungsmethode für große Einsparungen!

Intelligente Methodik - Ausgangslage
#1 Was ist Intelligenz?
#2 Bedingte Wahrscheinlichkeit?
#3 Restlebensdauer des Bestandes?
#4 Restlebensdauer nach Alter/Zustand?
#5 Was sind Neuronale Netzwerke?
#6 Schadensdetektion?

#1 Definition intelligent
Als Intelligenz kann die (menschliche) Fähigkeit bezeichnet werden aus Erfahrung zu lernen, sich an neue Situationen anzupassen, abstrakte Konzepte zu verstehen und die Umwelt zu beeinflussen. Künstliche Intelligenz befasst sich mit der Automatisierung intelligenten Verhaltens und maschinellem Lernen.
Fazit: Keine allgemeine Definition – aber Abwesenheit erkennbar!

#2 Bedingte Wahrscheinlichkeit
Bedingte Wahrscheinlichkeiten können in einer Kreuztabelle oder einem Pfaddiagramm dargestellt werden. Die Wahrscheinlichkeit des Eintrittes eines bedingten Ereignisses ergibt sich aus der Multiplikation der Wahrscheinlichkeit entlang der Pfade (z.B. P(𝑨 ̅∩𝑩)=1 Ausfall p.a. → Trefferquote Prüfer P(B)=?, Unnötiger Ersatz?).
Fazit: Auf nicht direkt beobachtbare Zusammenhänge schließen!

#3 Restlebensdauer überlebender Assets
Wenn von Restlebensdauer des Anlagenbestandes gesprochen wird ist tatsächlich die Restlebensdauer überlebender Assets gemeint. Während die mittlere Restlebensdauer aller Anlagen linear abnimmt, liegt die Restlebensdauer überlebender Anlagen mit zunehmendem Alter darüber, da bereits ausgefallenen Anlagen nicht enthalten sind.
Fazit: Höhere Restlebensdauer und besserer Zustand als Schnitt!

#4 Zustands- und altersbedingte Restlebensdauer
Sind der charakteristische Zustandsverlauf, die mittlere Lebensdauer sowie Ausfallsverteilung bekannt, kann die zustandsbedingte Restlebensdauer ermittelt werden. Dazu ist der charakteristische Zustandsverlauf durch die Grenzen des Zustandsbereichs zu skalieren und der Schwerpunkt des resultierenden Bereichs der Ausfallsverteilung zu ermitteln.
Fazit: Die Restlebensdauer nach Zustand und Alter ist berechenbar!

#5 Neuronale Netzwerke (NN)
Künstliche neuronale Netze bestehen aus Layern, deren Neuronen durch positiv und negativ gewichtete Verbindungen einen Einfluss ausüben. Wird ein Schwellenwert in der Aktivierungsfunktion erreicht, gibt das Neuron Informationen weiter. In der Trainingsphase lernt das Netzwerk durch Modifikation der Gewichte mit Lernregeln.
Fazit: Neuronale Netzwerke sind vor Anwendung richtig zu trainieren!

#6 Schadensdetektion (NN)
Wesentliche Anwendungsfelder im Ingenieurwesen sind u.a. die Erkennung wiederkehrender Muster in Bildmaterial ( z.B. Gesichter, Schäden) und die Prognose bei einer Vielzahl an Einflussfaktoren. Qualitätsmerkmal der Erkennung ist die Detektionsrate in der Testphase d.h. der Anteil richtig erkannter Informationen.
Fazit: Trainingsset und Detektionsrate sind entscheidend!

Modulare Methodik - Ausgangslage
#1 Was bedeutet modular?
#2 Vereinfachung Systeme?
#3 Zuverlässigkeit Elemente?
#4 Zuverlässigkeit Systeme?
#5 Asset Management Zyklus?
#6 Umsetzungsbeispiele?
#1 Definition modular
Im Systems Engineering können komplexe Aufgaben oder Systeme in einzelne in sich funktional geschlossene Einheiten gegliedert werden. Diese Einheiten oder Module erfüllen eine Aufgabe im Gesamtsystem und ermöglichen so eine effiziente Strukturierung bzw. sequenzielle oder parallele Bearbeitung je nach Ressourcen, Zeitplan und Priorität.
Fazit: Komplexe Aufgaben in überschaubare Bausteine zerlegen!

#2 Systemaufbau
In der Systemtheorie wird ein System als eine von der Umwelt abgrenzbare Entität bestehend aus Elementen definiert. Die Beschreibung realer komplexer Systeme erfordert Vereinfachungen und kann in Form von Blockdiagrammen für die Zuverlässigkeitsanalyse, Ereignisbäumen oder Pfaddiagrammen erfolgen.
Fazit: Zuverlässigkeitsanalyse von Systemen mit Blockdiagramm!
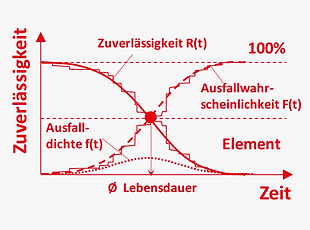
#3 Zuverlässigkeit von Elementen
Die Zuverlässigkeit R(t) von Elementen kann nach Zeit bzw. Belastung beschrieben werden und hängt direkt mit der Ausfallwahrscheinlichkeit
F(t) = 1 - R(t) und Ausfallsdichte f(t) zusammen. Die Bestimmung der Zuverlässigkeit kann über Alterungs- oder Belastungstests sowie über systematische Aufzeichnungen und statistische Analysen erfolgen.
Fazit: Systematische Aufzeichnungen für Zuverlässigkeitsanalysen!

#4 Zuverlässigkeit von Systemen
Je nach Art des Systems ist die Zuverlässigkeit eine andere Funktion als die der Elemente. Bei parallelen Systemen ist die Zuverlässigkeit erhöht, da nur ein Element überleben muss, während sie bei seriellen Systemen niedriger ist, da der Ausfall eines Elementes zum Systemausfall führt. Bei k aus n Elementen liegt das Ergebnis dazwischen.
Fazit: Die Summe kann schlechter/besser sein als die Teile!

#5 Asset Management Zyklus
Der Asset Management Prozess ist zyklisch aufgebaut und zielt auf eine ganzheitliche Betrachtung alle Phasen im Lebenszyklus ab. Der Zyklus besteht aus Bestands- und Zustandserfassung, Prognosen, Modellierung von Maßnahmenwirkung und Kosten, Optimierung, Budgetierung, Bauprogramm, Abnahme und Benchmarking.
Fazit: Logischer Kreislauf für systematische Verbesserung!

#6 Umsetzungsbeispiele
Wenn es keine guten Lösungen gibt, wird die Suche nach „best practises nicht sinnvoll sein. Die gezeigten methodischen Ansätze in Asset Management und Lebenszykluskostenrechnung sind auf Basis von Forschung und Anwendung entstanden. Jedes Vorhaben bietet die Gelegenheit innovative Ansätze zu erproben und weiterzuentwickeln.
Fazit: In Praxis und Vorhersage muss sich jede Theorie beweisen!


